The Parallel Processing Concept – Part I
In my book I summarize the statistical mechanics behind the dominating framework for animal space use models; mechanistic behaviour. This framework comes in two main “flavours”; with and without spatial memory. However, following this introduction the book is devoted to a third approach, based on non-mechanistic behaviour; called parallel processing. In a new series of blog posts, I start by showing how to discriminate between these three scenaria at the conceptual level
In fact, as shown in the Scaling cube (search Archive) I demarcate eight statistical-mechanical flavours of space use; called universality classes of space use, but let’s keep it simpler here.
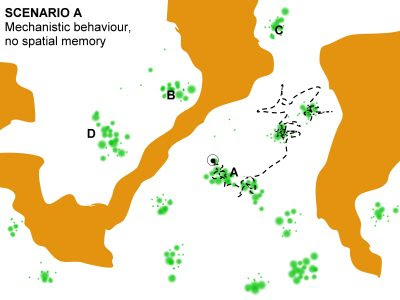First, consider a habitat playground like the one in the image to the right. White and brown area represents the matrix environment. White habitat is not selected for (basically, providing transit zones) while brown areas are landscape parts that are actively avoided. Green patches represent habitat elements – “resource patches” – that are selected for. The black dot represents the animal’s current location, and its surrounding circle represents an extreme simplification of the perceptual field at this location.
Mechanistic behaviour regards a process that in biophysical terms is compliant with a Markov process. In Scenario A of a mechanistic process (see image above) the actual path of an animal reflects the accumulation of spatial displacements from events that the individual has been confronted with as time goes by. For example, in this example the path resembles area restricted search (the classical ARS model). Under this condition movement in more convoluted in patches that is selected for and more uni-directional as the animal is searching for another resource patch.
Since many animals under a broad range of conditions show a tendency to constrain its space use (described as a home range), the general effect from memory map utilization should be implemented for the sake of better realism. Thus, consider Scenario B, where spatial memory has been introduced under the mechanistic modelling paradigm (as exemplified by Börger et al. 2008; van Moorter et al. 2009). Red-coloured patches represent memorized patches from previous visits.
In this variant of a mechanistic model a second circle following the moving animal is introduced. This circle demarcates previously visited patches that are considered relevant for a potential directed return from its present location, as the animal successively considers its next move during the short time increment that characterizes the actual Markov process. Like the perceptual field, the outer circle should also be considered a simplification of a field; i.e., its influence is reduced with the magnitude of its radius.The outer circle’s size reflects a “distance penalty” for returns from its present location to a previously visited and locally attractive patch (van Moorter et al 2009). Due to the successive updating of movement decisions, both circles follows the animal’s current position. The red path illustrates such a return event to patch A, initiated while the animal was in another patch and decided what to do next.
However, in our quest for improved realism we may still need to expand our modelling framework. In Scenario C I have introduced several circles, where the next larger circle is k times larger than the foregoing circle (in this example, k=2). Why this complication?
Consider that the animal has the cognitive capacity to execute goals at several temporal “resolutions” in parallel. For example, while following a short term goal to move to a nearby patch it may also have a more strategic goal to return to another patch within a larger time frame. As long as the short term goal is not in conflict with the more strategic goal, both are executed but at different time scales. Since distant returns generally require a coarser time resolution for it execution, this level of memory map utilization is represented by larger circles. The set of circles represents a simplification of a scale-free continuum of process rates.
If you “squeeze” the process scales into a single time resolution, you get the classic Markov (mechanistic) system design as described in Scenario B. Allowing for a range of process rates – as in Scenario C – introduces complex space use. As I describe in my book, there is a qualitative difference between complexity and complicatedness. Thus, parallel processing represents an extension of the mechanistic/Markovian framework, similar to modelling where non-linear functional relationships are generalization of linear (proportional) counterparts.
In follow-up posts I’ll explain why the parallel processing concept requires a theoretical extension of the traditional statistical mechanics. I will also show how a simple statistical analysis of GPS fixes may reveal to what extent the underlying space use behaviour has been compliant with either the mechanistic principles or the parallel processing principles. In other words, the analysis may differentiate between the scenaria A, B and C without having to study the actual behaviour at fine temporal resolutions.
REFERENCES
Börger, L., B. Dalziel, and J. Fryxell. 2008. Are there general mechanisms of animal home range behaviour? A review and prospects for future research. Ecology Letters 11:637-650.
Gautestad, A. O., L. E. Loe, and A. Mysterud. 2013. Inferring spatial memory and spatiotemporal scaling from GPS data: comparing red deer Cervus elaphus movements with simulation models. Journal of Animal Ecology 82:572-586.
van Moorter, B., D. Visscher, S. Benhamou, L. Börger, M. S. Boyce, and J.-M. Gaillard. 2009. Memory keeps you at home: a mechanistic model for home range emergence. Oikos 118:641-652.
In fact, as shown in the Scaling cube (search Archive) I demarcate eight statistical-mechanical flavours of space use; called universality classes of space use, but let’s keep it simpler here.
First, consider a habitat playground like the one in the image to the right. White and brown area represents the matrix environment. White habitat is not selected for (basically, providing transit zones) while brown areas are landscape parts that are actively avoided. Green patches represent habitat elements – “resource patches” – that are selected for. The black dot represents the animal’s current location, and its surrounding circle represents an extreme simplification of the perceptual field at this location.Mechanistic behaviour regards a process that in biophysical terms is compliant with a Markov process. In Scenario A of a mechanistic process (see image above) the actual path of an animal reflects the accumulation of spatial displacements from events that the individual has been confronted with as time goes by. For example, in this example the path resembles area restricted search (the classical ARS model). Under this condition movement in more convoluted in patches that is selected for and more uni-directional as the animal is searching for another resource patch.
- In this scenario, a return to patch A will happen by chance; similar to a future discover of patch C. Patches B and D are out of reach due to the repulsive brown area. In the long run, after “infinite” number of movement events, local staying times in respective sub-areas of the available arena (consider that we superimpose a virtual grid to demarcate sub-areas within the playground) will be positively correlated with the relative magnitude of resources in respective sub-areas. Thus, classical use/availability analyses should be expected to perform well.
In this variant of a mechanistic model a second circle following the moving animal is introduced. This circle demarcates previously visited patches that are considered relevant for a potential directed return from its present location, as the animal successively considers its next move during the short time increment that characterizes the actual Markov process. Like the perceptual field, the outer circle should also be considered a simplification of a field; i.e., its influence is reduced with the magnitude of its radius.The outer circle’s size reflects a “distance penalty” for returns from its present location to a previously visited and locally attractive patch (van Moorter et al 2009). Due to the successive updating of movement decisions, both circles follows the animal’s current position. The red path illustrates such a return event to patch A, initiated while the animal was in another patch and decided what to do next.
- In this scenario, a return to – for example – patch A from a distant location may happen either by chance or as a result of memory map utilization (directed return events). However, patches B and D are still out of reach. In the long run, after “infinite” number of movement events (including both exploratory moves and memory-dependent returns), the accumulation of local staying times in respective sub-areas of the available arena will be positively correlated with the relative magnitude of resources in respective sub-areas. This follows from standard statistical-mechanical system properties for mechanistic behaviour. Thus, classical use/availability analyses should also in this scenario be expected to perform well after some modification (accounting for the difference between green and red patches).
Consider that the animal has the cognitive capacity to execute goals at several temporal “resolutions” in parallel. For example, while following a short term goal to move to a nearby patch it may also have a more strategic goal to return to another patch within a larger time frame. As long as the short term goal is not in conflict with the more strategic goal, both are executed but at different time scales. Since distant returns generally require a coarser time resolution for it execution, this level of memory map utilization is represented by larger circles. The set of circles represents a simplification of a scale-free continuum of process rates.
- This processing continuum allows for discovering patches B and D, as indicated in the illustration. From the perspective of a coarser time scale and coarser space resolution, occasionally moving into what appears forbiddingly unattractive at finer resolutions may appear less forbidding and potentially give longer term positive reward in fitness terms due to more effective habitat exploration (observe that “coarser time scale” and “longer term” both reflect higher levels in the hierarchy of process rates). Hence, the parallel processing concept regards both exploratory moves and return moves. In this scenario, classical use/availability analyses should be expected to perform poorly unless alternative proxy variables for intensity of use are applied.
If you “squeeze” the process scales into a single time resolution, you get the classic Markov (mechanistic) system design as described in Scenario B. Allowing for a range of process rates – as in Scenario C – introduces complex space use. As I describe in my book, there is a qualitative difference between complexity and complicatedness. Thus, parallel processing represents an extension of the mechanistic/Markovian framework, similar to modelling where non-linear functional relationships are generalization of linear (proportional) counterparts.
In follow-up posts I’ll explain why the parallel processing concept requires a theoretical extension of the traditional statistical mechanics. I will also show how a simple statistical analysis of GPS fixes may reveal to what extent the underlying space use behaviour has been compliant with either the mechanistic principles or the parallel processing principles. In other words, the analysis may differentiate between the scenaria A, B and C without having to study the actual behaviour at fine temporal resolutions.
REFERENCES
Börger, L., B. Dalziel, and J. Fryxell. 2008. Are there general mechanisms of animal home range behaviour? A review and prospects for future research. Ecology Letters 11:637-650.
Gautestad, A. O., L. E. Loe, and A. Mysterud. 2013. Inferring spatial memory and spatiotemporal scaling from GPS data: comparing red deer Cervus elaphus movements with simulation models. Journal of Animal Ecology 82:572-586.
van Moorter, B., D. Visscher, S. Benhamou, L. Börger, M. S. Boyce, and J.-M. Gaillard. 2009. Memory keeps you at home: a mechanistic model for home range emergence. Oikos 118:641-652.