Animal Space Use

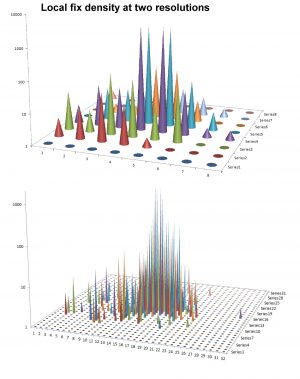
In my book I devote several chapters to explain, illustrate, simulate and mathematically formulate the parallel processing (PP) principle. PP represents the foundation of the extended statistical-mechanical framework that I propose as necessary to model complex space use more realistically. In this Part II of the PP description I elaborate further on this unfamiliar approach, which represents an alternative to the standard “Markov process” (mechanistic) methods in movement ecological theory. Hopefully the reader of my book and these supplementary blog posts will manage the difficult task to be both critical and open-minded. After all, I have formulated several testable hypotheses, where the null hypothesis is the standard framework and the alternative hypothesis is the PP-compliant process. Several pilot tests on real animal space use are presented in my book and in our papers, lending support to a PP kind of space use; spatio-temporal memory utilization in combination with a multi-s

In a previous blog post I summarized an alternative approach to estimate local habitat selection, based on the individual’s characteristic scale of space use, CSSU, rather than local density of fixes (the utilization distibution, UD). In the present post I compare the density-based UD with local variation of CSSU in the context of habitat selection, using both simulated and real space use. Despite being critical to the traditional UD approach I also argue that density of fixes may still reveal important properties of value for ecological inference, and I describe this by an example. In my book I argue strongly against using the traditional UD model as a proxy for strength of intra-home range habitat selection. The UD reflects local density of fixes. The reason for my critique is the UD’s intrinsically self-similar (fractal) structure under realistic home range conditions, while theoretical UD models are inherently non-fractal (“statistically smooth surface at fine resolutions”). The