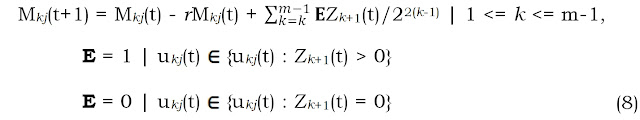Animal Space Use

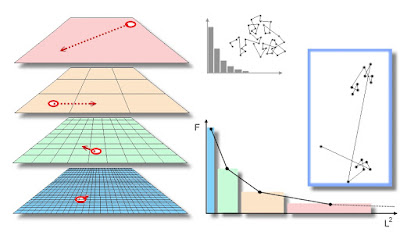
In a recent post I summarized the Zoomer model, a population level version of Multi-scaled random walk (MRW). Interestingly (in fact, thrillingly!) I just discovered a recent paper on the statistical properties of movement of the B6 strain of laboratory mice (Shoji 2016), which indirectly supports an important statistical-mechanical assumption both under the zoomer concept and the MRW. Before turning towards movement of mice, I recap a basic property of the Zoomer model, and its coherence with the complementary individual-level process. The illustration above is copied from Gautestad and Mysterud (2005), and illustrates the zoomer principle from the individual level; i.e., from the perspective of Multi-scaled random walk (MRW). To the left: individual zoomers are in the process of relocating themselves at length L at respective spatial scales (indicated by virtual grid resolutions) during a given time period T=M*t, where t is the unit time scale and series length M is large. Cons...

Presented for the first time in my book, Multi-scaled random walk (MRW) hereby also has a complementary formulation for population kinetics, “the Zoomer model” (see Chapter 6. Modelling parallel processing). While population dynamics primarily is occupied with the time scale of seasons, years and generation times, population kinetics is typically also including the shorter time range of intra-season redistribution of individuals. In other words, this concept also covers higher-frequency and finer-grained spatio-temporal variability of a population’s distribution – as a mixture of intrinsic and extrinsic factors – in a more explicit manner than traditional population dynamical modelling. If movement is “simple”, i.e., obeying classic diffusion laws and thus the mean field principle at the population level, the effect from individual-level system details may conveniently be “averaged out”, allowing for quite simply-structured models. In physics and probability theory, mean field th...

One particular class of complex space use – Multi-scaled random walk (MRW) – implies that movement is influenced both by spatially explicit memory utilization and temporally multi-scaled goal execution; in short, it covers spatially explicit strategic locomotion, which may be processed over a range of temporal scales (the parallel processing conjecture; see the December post that summarizes the scaling cube). In this Part II I continue to focus on statistical-mechanical properties I elaborate on the entropy aspect of movement. Specifically, I describe how this key property may be coherently maintained – albeit in a surprising manner – even in the non-classic kind of space use, as represented by the MRW model. According to the standard framework, one should not expect a change of entropy when “zooming” in and out of a given system of a given extent. This property will now be rattled as we move to the scale-free condition. First, the classic system condition. Consider that a virtu...