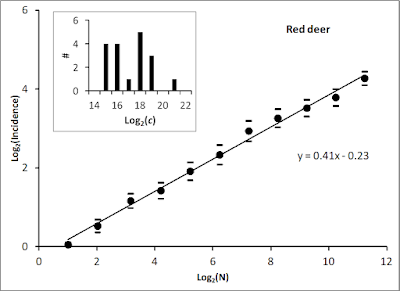
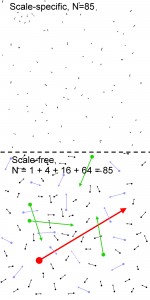
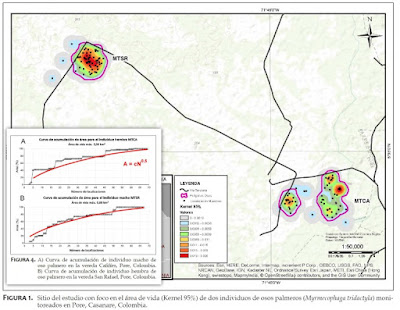
Homogeneous or Heterogeneous Environment?
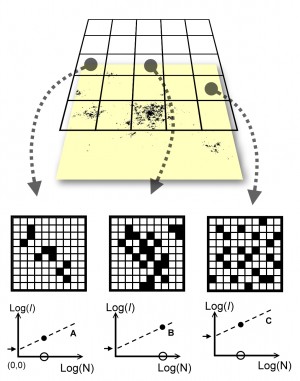
When simulating animal space use – whether at the level of individuals or populations – some of the first conditions to define regard the attributes of the arena. The environment may be simple (homogeneous) or complicated (heterogeneous). As always the choice is a matter of weighing model simplicity against realism. However, another dimension of this choice is often overlooked. Animal space use is always a mixture of intrinsic and extrinsic driving forces. Thus, by simulating in a homogeneous environment one may to some extent disentangle these aspects by studying the intrinsic dynamics first and then – in follow up simulations – adding extrinsic variability. This is an important point to stress, since simple models in homogeneous environment have occasionally been criticized for lack of realism. As an example of how simplicity may contribute to important insight, consider traditional home range simulations (the convection model), observed at a statistical-mechanical temporal scale...