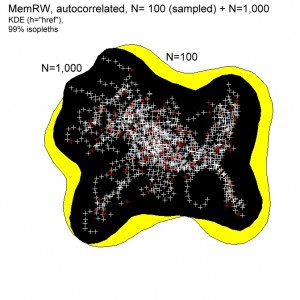
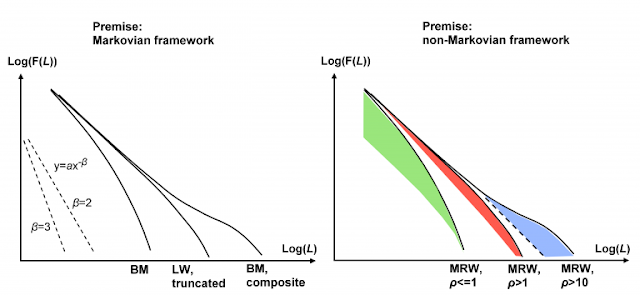
A Statistical-Mechanical Perspective on Site Fidelity – Part V
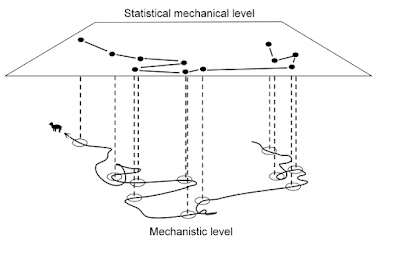
Two important statistical-mechanical properties need to be connected to the home range concept under the parallel processing postulate; micro- and macrostates. When a system is in its equilibrium state, (a) all microstates are equally probable and (b) the observed macrostate is the one with the most microstates. The equilibrium state implies that entropy is maximized. First consider a physical system consisting of indistinguishable particles. For example, in a spatially constrained volume G of gas (a classical, non-complex system) that consists of two kinds of molecules, at equilibrium you expect a homogeneous mixture of these components. At every virtually defined locality g within the volume, the local density (N/g) of each type of molecule is expected to be the same, independently of the resolution of the two- or three-dimensional virtual grid cell g we use to test this prediction. This homogeneous state is in compliance with a prediction based on the most probable macrostate fo...