Animal Space Use

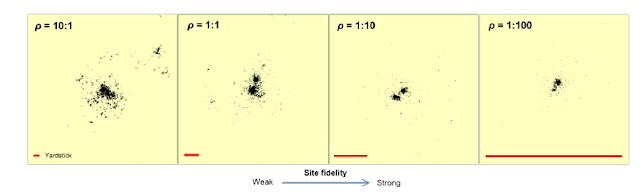
Back in 1994 I enjoyed an unforgettable and extremely inspiring 2-month stay at University of Tennessee, visiting professor Stuart L. Pimm (Department of Ecology and Evolutionary Biology) and Professor Mike L. Pelton (Department of Forestry, Wildlife and Fishery). During some hectic weeks I worked on transforming the mathematical formulation of the Zoomer model for complex population dynamics into a spatially explicit simulation model (Stuart’s lab) in parallel with interaction with many dedicated students of the biology and ecology of black bear Ursus americanu s (Mike’s lab).The Zoomer model is published in my book and already commented on this blog. Regarding the stay at Mike’s lab we published a test on the bears’ general space use, where we found close compliance with the Multi-scaled random walk model, MRW (Gautestad et al. 1998). In this post I revisit the black bear data and find this model’s additional potential to cast light on behavioural ecology in a wildlife management c

While stronger intensity of space use in the standard (Markovian/mechanistic) biophysical model framework is equal to the proxy variable fix density, density=N/area, the complex system analogue is 1/c. This alternative expression for intensity is derived from from the Home range ghost formula I = cN 0.5 = c √N). Below I illustrate the biophysical difference between the two intensity concepts by a simple Figure and some basic mathematics of the respective processes. The extended statistical mechanics of complex space use underscores the importance of estimating and applying a realistic spatial resolution, close to the magnitude of CSSU, when analyzing individual habitat utilization within various habitat classes. The traditional density variable for space use intensity will invoke a large noise term and even spurious results in ecological use/availability analyses of home range data. In statistical-mechanical terms, one of the main discrepancies between the traditional space use mode

In light of the recent insight that individuals of a population generally seem to utilize their environment in a multi-scaled and even scale-free manner, the metapopulation concept needs a critical evaluation. Even more so, since many animals under a broad range of ecological conditions are simultaneously mixing scale-free space use with memory map-based site fidelity. In fact, both properties, multi-scaled movement and targeted return events to previous locations, undermine key assumptions of the metapopulation concept. Levins (1969) model of “populations of populations” – termed metapopulation – rattled many corners of theoretical and applied ecology, despite previous knowledge of the concept from the groundbreaking research by Huffaker (1958) and others (Darwin, Gause, etc.). Since then, Ilkka Hanski (1999) and others have produced broad theoretical and empirical research on the metapopulation concept. The Levins model describes a metapopulation in a spatially implicit manner, w

Ideally, when studying ecological aspects of an individual’s whereabouts based on (for example) series of GPS fixes, N should not only be large. The series of fixes should also be non-autocorrelated to ensure statistically independent samples of space use. Since these two goals are difficult to fulfill simultaneously (the latter tend to undermine the former), two workarounds are common. Either the autocorrelation issue is ignored albeit recognized, or space use is analyzed by path analytical methods rather than the more classical use-availability approach. Both workarounds have drawbacks. In this post I show for the first time a surprisingly simple method to compensate for the oversampling effect that leads to autocorrelated series of fixes. Again, as in Part II of this series, I focus on how to improve realism and reduce the statistical error term when studying ecological aspects of habitat selection, given that data compliance with the MRW framework has been verified (see, for exa

Through the history of ecological methods, local intensity of habitat use has been equalized with local density of relocations. Using relative density as a proxy variable for intensity of habitat use rests on a critical assumption which few seems to be aware of or pay attention to. In this second post on Multi-scaled random walk (MRW) applications for ecological inference I describe a simple method, which rests on an alternative assumption with respect to space use intensity, applicable under quite broad behavioural and ecological conditions. One immediate proposal for application is analysis of habitat selection. First, consider counting number of GPS fixes, N, within respective area segments of a given habitat type h, A h1 , A h2 , …, A hi , …A hk , and calculating the average N pr. area unit of type h. Next, consider comparing this density D h with another density within a second habitat type j; i.e., D j , using the same area scale for comparison. If Dh>Dj one traditionally

In this “MRW and Ecology” series of posts I present summaries of simple ecological methods – based on alternative basic assumptions – for analysis of common ecological aspects of animal space use. These proposals are spin-offs of the first direction of research to explicitly break out of the Markovian strait-jacket in the present context. A broadened analytical approach – involving a qualitative shift of direction – is in my view clearly needed, as documented by the rapidly growing line of high quality and deep-level analyses of empirical data now appearing. For such an alternative direction the parsimonious Multi-scaled random walk model (MRW) may provide a feasible starting point. Over the years the MRW approach has been successfully tested empirically against the prevailing paradigm’s basic assumptions, or indirectly supported by alternative interpretations of respective analyses of space use and movement. Thus, now it’s time to step forward from testing behavioural feasibility of

Random walk is one of the most sticky concepts of movement ecology. Unfortunately, this versatile theoretical model approach to simplify complex space use under a small set of movement rules often leads to confusion and unnecessary controversy. As pointed out by any field ecologist, unless an individual is passively shuffled around in a stochastic sequence of multi-directional pull and push events, the behavioural response to local events and conditions is deterministic! An animal behaves rationally. It successively interprets and responds to environmental conditions – within limits given by its perceptive and cognitive capacity – rather than ignoring these cues like a drunken walker. Any alternative strategy would lose in the game of natural selection. Still, from a theoretical perspective an animal path may still be realistically represented by random walk – given that the randomness is based on properly specified biophysical premises and the animal adhere to these premises. Outs

The Multi-scaled random walk (MRW) model defines a specific dispersal kernel for animal movement; a power law, which is qualitatively different from standard theory (a negative exponential function). Alcaide et al. (2009) analyzed long-term ringing programmes of the lesser kestrel Falco naumanni in Western Europe, and showed results from re-encounters of 1308 marked individuals in Spain. They found that most first-time breeders settled within 10 km from their natal colony (i.e., a strong philopatric tendency), with a negative association between natal dispersal and geographical distance. While Alcaide et al . (2009) were mainly concerned with gene flow and population effects, here I take a deeper look at their dispersal data and find strong support for MRW-compliant behaviour in the natal dispersal data. Indirectly, this pattern at the individual level also supports the MRW-analogue at the population level, the Zoomer model (Gautestad 2015). I allow myself to copy their Figure 1, s

The theoretical framework of the traditional space use models (“the Paradigm”) shows strong mathematical coherence between individual movement and its population level representation. Basically (in its simplest and most parsimonious form), standard random walk representing individual statistics is compliant with standard diffusion representing population statistics. Further, the trunk of the toolbox of statistical methods in space use ecology is also resting on assumptions from the Paradigm. However, the Paradigm and its large family of sophisticated sub-models is now under increasing attack from many directions – directly or indirectly – due to the growing pool of empirical results that cast doubt on its common, core assumptions. For example, recent analyses of the snail kite Rostrhamus sociabilis plumbeus in Florida indicate that individuals of this dietary specialist show a surprising capacity to rapidly adapting to changing conditions over a large range of spatial scales from loca

Merkle et al. (2014; 2017) have developed and tested a sophisticated memory-including patch selection model for free-ranging bison ( Bison bison ). Some of the empirical results add support to the Multi-scaled Random Walk (MRW) model (Gautestad and Mysterud 1995, 2005; Gautestad 2015), while other aspects require further details of the bison data to evaluate the potential for full compliance. In Merkle et al .’s simulation model; which is described by both a Lagrangian and a quasi-Eulerian variant (integro-difference equation, leading to similar results), animals use spatial and attribute memory to choose food patches based on three components: whether or not they have previously visited them, their reference point of patch profitability derived from recent foraging experience, and their memory of the profitability of each previously visited patch. First, the results confirm home range as an emergent property of spatial memory. Animals returning to previously visited patches wit

Recent research on animal migration continue to challenge the paradigm of assuming relatively straight-line routes between start locations and respective targets, as shown in a study on blackpoll warblers Setophaga striata (Brown and Taylor 2017). The warblers had a surprisingly high degree of back-and-forth displacements during migration; apparently more than can be explained by adjusting steps to local habitat attributes along the path. Migration regards an endpoint on the scale continuum from short term movement bouts to long-distance seasonal displacements. Thus, one of the core challenges for more realistic models in wildlife ecology regards how to conceptualize and then formulate (in short: understand from simulations and from testing model predictions) the multi-scaled cognitive processing of environmental information and displacement decisions in animals. This insight should account for all time resolutions up to the migration scale. From Insecta to Aves and Mammalia , i