On the Paradox of Mechanistic Movement Models
Mechanistic design is still dominating animal space use modelling. As the readers of my papers, book and blog have understood I’m very critical to this framework. In particular, because both mechanics and standard statistical mechanics – due to their dependence on Markovian dynamics seem to be unable to implement memory-influenced movement in a realistic manner. Thus, paradoxes abound. Unfortunately most theoreticians in movement ecology either do not care or do not know how to approach this issue. In this post I seek to pinpoint the most basic challenge, and how it may be potentially resolved by exploring a qualitatively new direction of modelling.
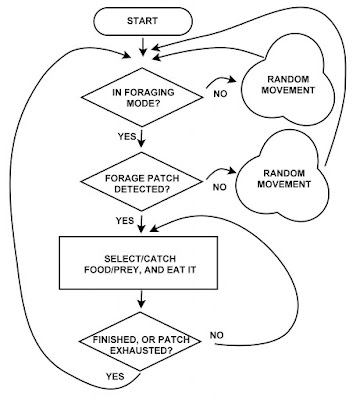
Consider the standard, simplified illustration of animal foraging, which takes up much of an individual’s focus during a day. At each time increment the behaviour adheres to rules under the mathematical framework of a low order Markovian process. A similar diagram could have been shown for other behavioural modes; like looking for a mate, seeking a shelter for resting, and so on. In short, mechanistic behaviour describes rules, which may be executed deterministically, stochastically or as a mixture. The key point is that the process in model terms is described at a specific temporal resolution. In other words, each “Start” in the illustration to the right regards execution of behaviour during the current time increment; i.e., at the current moment at the given unit time scale.
A Markov chain is a stochastic model describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event. In probability theory and related fields, a Markov process, named after the Russian mathematician Andrey Markov, is a stochastic process that satisfies the Markov property (sometimes characterized as “memorylessness”). Roughly speaking, a process satisfies the Markov property if one can make predictions for the future of the process based solely on its present state just as well as one could knowing the process’s full history, hence independently from such history, that is, conditional on the present state of the system, its future and past states are independent.
The alternative approach to modelling animal space use – MRW and the Zoomer model – is advocated my papers, my book and on this blog. These contributions also provide several simple methods to test model compliance – Markovian vs. non-Markovian processing – using your own data.
It is of course up to each ecologist to ignore these warning signs for the realism of standard dynamic modelling of animal movement and space use, but be aware that an increasing number of physicists are now drawn towards this field of research. In an upcoming post I will summarize some of these recent developments, which in large part seem to have been initially inspired by my MRW simulations that began appearing in papers about 15 years ago**.
NOTES
*) Biological and ecological conditions may constrain the utilization to a more narrow range, for example when or where the environment is relatively unpredictable. In that case the value of old information i rapidly diminishing as a function of time.
**) In fact, the first simulations of MRW were published already in my PhD thesis back in 1998.
Consider the standard, simplified illustration of animal foraging, which takes up much of an individual’s focus during a day. At each time increment the behaviour adheres to rules under the mathematical framework of a low order Markovian process. A similar diagram could have been shown for other behavioural modes; like looking for a mate, seeking a shelter for resting, and so on. In short, mechanistic behaviour describes rules, which may be executed deterministically, stochastically or as a mixture. The key point is that the process in model terms is described at a specific temporal resolution. In other words, each “Start” in the illustration to the right regards execution of behaviour during the current time increment; i.e., at the current moment at the given unit time scale.
A Markov chain is a stochastic model describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event. In probability theory and related fields, a Markov process, named after the Russian mathematician Andrey Markov, is a stochastic process that satisfies the Markov property (sometimes characterized as “memorylessness”). Roughly speaking, a process satisfies the Markov property if one can make predictions for the future of the process based solely on its present state just as well as one could knowing the process’s full history, hence independently from such history, that is, conditional on the present state of the system, its future and past states are independent.
https://en.wikipedia.org/wiki/Markov_chain
Animals including at least mammals, birds, reptiles, amphibians and fish (apparently also many species of invertebrates), have a cognitive capacity both to orient themselves in space and to relate to a larger or lesser degree to past experiences from visited space. For example, a home range is an emergent property of this capacity, where the animal under specific biological and ecological circumstances prefers to revisit some of its previously visited locations more frequently than by chance.
Animals including at least mammals, birds, reptiles, amphibians and fish (apparently also many species of invertebrates), have a cognitive capacity both to orient themselves in space and to relate to a larger or lesser degree to past experiences from visited space. For example, a home range is an emergent property of this capacity, where the animal under specific biological and ecological circumstances prefers to revisit some of its previously visited locations more frequently than by chance.
Hence, my definition of a home range is a space use process where the individual is crossing its previous path non-randomly. In this manner, the problematic notion of a specific home range area is avoided. Focus is instead redirected towards site fidelity, but in a manner that is postulated to be non-mechanistic (the parallel processing conjecture; search Archive).
There have been many proposals for modelling spatial memory, based on the standard principles of the mechanistic (Markovian) framework. For example, the animal could cognitively store its experience from successive locations along its path with respect to local food attributes and the location of these experiences (memory map utilization). This mixed bag of experiences is then repeatedly recalled in present-moment (real time) decisions what to do next, in a sequential manner. The execution of behaviour happens along a trailing time window; i.e., the model design is set to assume the behaviour is a high order rather than low order Markovian process. However, by computational necessity older experiences further back than a given memory capacity is lost. There is thus a logical limit to the trailing window of memory utilization. In other words, the trailing window becomes smaller and smaller relative to the total span of the process itself as time goes by.
There have been many proposals for modelling spatial memory, based on the standard principles of the mechanistic (Markovian) framework. For example, the animal could cognitively store its experience from successive locations along its path with respect to local food attributes and the location of these experiences (memory map utilization). This mixed bag of experiences is then repeatedly recalled in present-moment (real time) decisions what to do next, in a sequential manner. The execution of behaviour happens along a trailing time window; i.e., the model design is set to assume the behaviour is a high order rather than low order Markovian process. However, by computational necessity older experiences further back than a given memory capacity is lost. There is thus a logical limit to the trailing window of memory utilization. In other words, the trailing window becomes smaller and smaller relative to the total span of the process itself as time goes by.
However, as I’ve documented over a large range of simulation examples where theory and empirical results are compared, the space use pattern as seen in large sets of individual relocations (e.g., in telemetry/GPS-based studies) do not seem to comply with the basic statistical properties of mechanistic/Markov behaviour.
Examples of empirical results that undermine the Markovian model design and lend support to the alternative Multicaled random walk model (MRW):
- Fowler’s Toads: the MRW Model Gains Additional Support (blog post: July 21, 2017). The probability of return and/or the choice of refuge were distance-dependent (Marchand et al. 2017, p 68). In other words, they conclude that memory map utilization as defined in MRW in its generic form explained the data better than the more “biologically intuitive” variants.
- Patch Use by Bison in Canada: Memory and Habitat Exploration (blog post: August 03, 2017). Bison chose recently visited meadows as strongly as meadows visited farther into the past. In other words, memory decay was small, in compliance with the generic MRW model.
Animals seem to have a capacity for long term and spatially explicit memory utilization* well beyond the time scale of any high order Markov model. Simple statistical analyses from spin-offs under the alternative statistical-mechanical model designs reveal that these animals also relate to their environment in a scale-free manner, rather than the intrinsically scale-specific constraint of processing that by necessity follows from the standard or high order Markovian designs.
The alternative approach to modelling animal space use – MRW and the Zoomer model – is advocated my papers, my book and on this blog. These contributions also provide several simple methods to test model compliance – Markovian vs. non-Markovian processing – using your own data.
It is of course up to each ecologist to ignore these warning signs for the realism of standard dynamic modelling of animal movement and space use, but be aware that an increasing number of physicists are now drawn towards this field of research. In an upcoming post I will summarize some of these recent developments, which in large part seem to have been initially inspired by my MRW simulations that began appearing in papers about 15 years ago**.
NOTES
*) Biological and ecological conditions may constrain the utilization to a more narrow range, for example when or where the environment is relatively unpredictable. In that case the value of old information i rapidly diminishing as a function of time.
**) In fact, the first simulations of MRW were published already in my PhD thesis back in 1998.