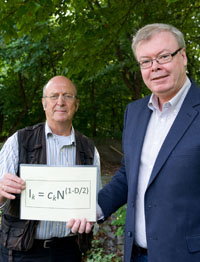Parallel Processing: Towards a Broadened Biophysics of Space Use, Part II
When I returned to the University of Oslo in 1990 to explore alternative pathways towards complex dispersion of populations it was natural to start out by orbiting around the Department of biology’s division that focused on population dynamical modelling. However, what became increasingly obvious was a tension that grew up between my choice of off-piste approaches, the introduction of rather unorthodox concepts and on the other side meeting a culture that stubbornly focused on the classical mathematical and statistical toolbox. I simply could not find satisfactory local support for working on scale-free dispersal processes under these terms, despite what I observed as thoroughly and broadly documented instances of such paradigm-breaking behaviour in the hundreds of papers surrounding confirmation of – for example – Taylor’s power law and fractal-patterned population dispersion. The theoretical culture was shying away from exploring a series of paradoxes that in my view were crying for an entirely novel approach. Thus, luckily in 1992 I knocked on Ivar Mysterud’s door further down the same corridor.
Ivar (now Professor emeritus) was mentor of my Master’s degree on a population of tawny owl Strix aluco, Now I sat in his office again, advocating my ideas for a PhD on animal space use in broader terms and how I felt it was necessary to drill into behavioural ecology at the individual level to seek solutions to the paradoxical dispersion processes in real populations. Characteristically for Ivar, he was immediately positive to such an endeavor that was aiming at some rather unfamiliar theoretical terrain. The more off-piste, the better! He already had concluded from his own field experience that completely new approaches were probably needed. But where to find them? Not in standard text books. Neither in contemporary papers that were influencing animal movement and habitat selection those days.
Right: Ivar Mysterud (left) and myself, displaying a novel equation that links home range utilization to to its fractal properties. From a 2010 article in the Norwegian resarch magazine Apollon (https://www.apollon.uio.no/artikler/2010/biologi.html). Photo: Francesco Saggio.
With Ivar’s very solid background as field ecologist in wildlife behaviour and management, he had already struggled in practical terms with analyzing animal space use complexity, in particular related to the aspects of home range behaviour. He offered me both an office and a four year scholarship to work freely (!) on whatever successively emerged as the most promising path forward. Best of all, Ivar’s and his students’ telemetry data on habitat use by free-ranging sheep Ovis aries were made available. He also ensured contact with his good friend Mike Pelton, professor at the University of Tennessee, where we were allowed to work on his lab’s extensive material on black bear Ursus americanus movement.
Within a year following the toggle from population kinetics to individual space use the first “metaphysical” property of the sheep data emerged from our analyses under the new terms (Gautestad and Mysterud 1993), including frequent and inspirational rounds on the office’s too small blackboard.
A catchy new concept emerged, “the Home range ghost” (Gautestad and Mysterud 1995).
For the initial 1993 paper the minimum convex polygon method* was used to study home range size as a function of sample size of telemetry fixes, n, including all ‘outliers’ available (more proper methods in follow-up works confirmed the same “ghost” aspects). The data were found to be satisfactorily non-auto-correlated at the given sampling intervals of several hours between successive relocations (fixes).
Then, what was the “metaphysical” Home range ghost property? For a start, consider demarcating space use from a total sample of N fixes using two protocols; (a) samples of n fixes (nmin < n <= N) that are drawn uniformly from the pool N, and (b) samples of n fixes that represent continuous series (time-close segments) from the total path of N fixes.
Ordinary theory and common sense predicted that the A(n) curves for home range area A from both methods should be quite overlapping, given that the fixes were temporally non-auto-correlated. In other words, n fixes from uniform sampling were expected to show similar A(n) as continuous sampling series. Otherwise, the latter should show smaller A for a given n. Further – again from the home range paradigm – the A(n) should be expected to flatten out towards an area asymptote for larger A.
The sheep data told us another story.
First, the asymptote of A(n) was not found (Figure 5a, to the left). In fact, with log-log scaled axes the function satisfied a straight line with slope z about 0.5; i.e., a scale-free power law log(A) = log(c) + z*log(n). Despite large sample size N available, the area demarcation grew proportionally with square root of N rather than approaching an asymptote. Second, despite the observed non-asymptotic function, the two sampling methods “uniform over N” and “sections within N” overlapped! That was strange, indeed.
A similarly strange power law pattern with z=0.5 was also found in Mike’s and his students material on black bear (Gautestad et al. 1998), which I recently also re-confirmed using latest methods of the Home range ghost theory (search Archive: "MRW and ecology part VI: black bear home ranges revisited"). In a meta-analysis of A(N) data from many species, taxa and ecological conditions, the overall result also confirmed the same power law with z≈0.5 (Gautestad and Mysterud 1994).
In short, we were able to show scale-free space use by applying the relatively new concepts of statistical fractals (Mandelbrot 1983, Feder 1988). But what was most explosive in our results were a property of space use that resonated well with the strange, apparently “metaphysical” property of sycamore aphids with respect to “time-independent” and “scale range dependent” pattern, like seen in 1/f noise spectra and in a subsection of Taylor’s power law (see Part I of this 2-part post). This time from analysis of individual space use rather than population dispersion.
NOTE
*) The MCP method, which was quite dominant in home range analyses at the time, was replaced by more robust statistical procedures in the follow-up work.
REFERENCES
Gautestad, A. O. and I. Mysterud. 1993. Physical and biological mechanisms in animal movement processes. J. Appl. Ecol. 30:523-535.
Gautestad, A. O. and I. Mysterud. 1994. Fractal analysis of population ranges: methodological problems and challenges. Oikos 69:154-157.
Gautestad, A. O. and I. Mysterud. 1995. The home range ghost. Oikos 74:195-204
Gautestad, A. O., I. Mysterud, and M. R. Pelton. 1998. Complex movement and scale-free habitat use: testing the multi-scaled home range model on black bear telemetry data. Ursus 10:219-234.
Ivar (now Professor emeritus) was mentor of my Master’s degree on a population of tawny owl Strix aluco, Now I sat in his office again, advocating my ideas for a PhD on animal space use in broader terms and how I felt it was necessary to drill into behavioural ecology at the individual level to seek solutions to the paradoxical dispersion processes in real populations. Characteristically for Ivar, he was immediately positive to such an endeavor that was aiming at some rather unfamiliar theoretical terrain. The more off-piste, the better! He already had concluded from his own field experience that completely new approaches were probably needed. But where to find them? Not in standard text books. Neither in contemporary papers that were influencing animal movement and habitat selection those days.
With Ivar’s very solid background as field ecologist in wildlife behaviour and management, he had already struggled in practical terms with analyzing animal space use complexity, in particular related to the aspects of home range behaviour. He offered me both an office and a four year scholarship to work freely (!) on whatever successively emerged as the most promising path forward. Best of all, Ivar’s and his students’ telemetry data on habitat use by free-ranging sheep Ovis aries were made available. He also ensured contact with his good friend Mike Pelton, professor at the University of Tennessee, where we were allowed to work on his lab’s extensive material on black bear Ursus americanus movement.
Within a year following the toggle from population kinetics to individual space use the first “metaphysical” property of the sheep data emerged from our analyses under the new terms (Gautestad and Mysterud 1993), including frequent and inspirational rounds on the office’s too small blackboard.
A catchy new concept emerged, “the Home range ghost” (Gautestad and Mysterud 1995).
For the initial 1993 paper the minimum convex polygon method* was used to study home range size as a function of sample size of telemetry fixes, n, including all ‘outliers’ available (more proper methods in follow-up works confirmed the same “ghost” aspects). The data were found to be satisfactorily non-auto-correlated at the given sampling intervals of several hours between successive relocations (fixes).
Then, what was the “metaphysical” Home range ghost property? For a start, consider demarcating space use from a total sample of N fixes using two protocols; (a) samples of n fixes (nmin < n <= N) that are drawn uniformly from the pool N, and (b) samples of n fixes that represent continuous series (time-close segments) from the total path of N fixes.
The sheep data told us another story.
A similarly strange power law pattern with z=0.5 was also found in Mike’s and his students material on black bear (Gautestad et al. 1998), which I recently also re-confirmed using latest methods of the Home range ghost theory (search Archive: "MRW and ecology part VI: black bear home ranges revisited"). In a meta-analysis of A(N) data from many species, taxa and ecological conditions, the overall result also confirmed the same power law with z≈0.5 (Gautestad and Mysterud 1994).
In short, we were able to show scale-free space use by applying the relatively new concepts of statistical fractals (Mandelbrot 1983, Feder 1988). But what was most explosive in our results were a property of space use that resonated well with the strange, apparently “metaphysical” property of sycamore aphids with respect to “time-independent” and “scale range dependent” pattern, like seen in 1/f noise spectra and in a subsection of Taylor’s power law (see Part I of this 2-part post). This time from analysis of individual space use rather than population dispersion.
NOTE
*) The MCP method, which was quite dominant in home range analyses at the time, was replaced by more robust statistical procedures in the follow-up work.
REFERENCES
Gautestad, A. O. and I. Mysterud. 1993. Physical and biological mechanisms in animal movement processes. J. Appl. Ecol. 30:523-535.
Gautestad, A. O. and I. Mysterud. 1994. Fractal analysis of population ranges: methodological problems and challenges. Oikos 69:154-157.
Gautestad, A. O. and I. Mysterud. 1995. The home range ghost. Oikos 74:195-204
Gautestad, A. O., I. Mysterud, and M. R. Pelton. 1998. Complex movement and scale-free habitat use: testing the multi-scaled home range model on black bear telemetry data. Ursus 10:219-234.