Patch Use by Bison in Canada: Memory and Habitat Exploration
Merkle et al. (2014; 2017) have developed and tested a sophisticated memory-including patch selection model for free-ranging bison (Bison bison). Some of the empirical results add support to the Multi-scaled Random Walk (MRW) model (Gautestad and Mysterud 1995, 2005; Gautestad 2015), while other aspects require further details of the bison data to evaluate the potential for full compliance.
In Merkle et al.’s simulation model; which is described by both a Lagrangian and a quasi-Eulerian variant (integro-difference equation, leading to similar results), animals use spatial and attribute memory to choose food patches based on three components: whether or not they have previously visited them, their reference point of patch profitability derived from recent foraging experience, and their memory of the profitability of each previously visited patch.
First, the results confirm home range as an emergent property of spatial memory. Animals returning to previously visited patches with a higher probability than path crossing by chance leads to constrained space use even without a central place attraction force or borderline repellence. In compliance with both MRW (Gautestad et al. 1998; Gautestad and Mysterud 2005) and other memory-implementing models (e.g., van Moorter 2009; Nabe-Nielsen et al. 2013) bison re-visits its memorized patches to a high degree.
Second, bison differentiates (to varying degree) between experienced patch profitability and the quality of the current patch when choosing which patch to return to. While the basic MRW formulation treats all previously visited locations along a path as equal (and thus let returns happen randomly), this “homogeneous environment” simplification is trivially extended with better realism by defining a heterogeneous habitat for the model execution (e.g., Gautestad and Mysterud 2013; see image below). In short, since patches with high profitability can be assumed to be positively correlated with longer local staying time, the MRW model’s Characteristic Scale of Space Use (CSSU) parameter can be defined to vary accordingly. Hence, the local path density (number of locations pr. unit area) in superior patches will tend to be higher than average density. Consequently, even when the animal returns randomly and with equal relative weight to any previous location along the total path, the target location for such return events will tend to be over-represented in high quality patches. Further, when averaging over all visited patches, the basic MRW model is assumed to represent the average CSSU for the given space use extent. Thus, when studying over-all space use properties rather than (for example) intra-home range patch selection, the basic MRW model with homogeneous environment (constant CSSU) satisfies the Occam’s razor principle.
Third, bison chose meadows visited far back in time as strongly as recently visited meadows. In other words, memory decay was small. This is also a basic property of MRW. However, it could trivially be extended by allowing for varying degree of memory decay through time-dependent return probability to previously visited locations (Gautestad and I. Mysterud 2006; Gautestad and A. Mysterud 2013).
Fourth, Merkle et al. (2017) argue well for space use where targeted (memory-based) returns should be expected to be combined with random exploration. “…a certain amount of random patch use is necessary to avoid frequent returns to relatively poor-quality patches, or avoid being caught in a relatively poor quality area of the landscape” (p185). Bison data confirm this mixture of targeted returns and exploratory bouts, in compliance also with the MRW model.
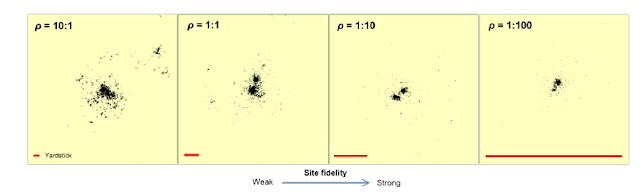
See conceptual illustration of varable CSSU above, showing our simulated scenaria under MRW and infinite memory horizon, where frequency of return steps is increasing by a factor of 10 per display from left towards right. The embedded red line in the lower part of each panel shows the spatial scale (for example, 1 km) for the respective arenas. For a given accumulated movement length (total path), MRW with a smaller return interval on average covers a smaller area than under condition of a larger return interval (smaller frequency of return). Thus, local density; locations pr. standardized spatial unit embedding at least one location, also increases accordingly. From Gautestad and Mysterud (2013).
What is missing from the bison results? Unfortunately, in order to test if bison confirms MRW-like space use relative to other memory-based models the data needs to be analysed for other properties. For example, the basic MRW model has two main components; (1) occasional return to previously visited patches, and (2) exploratory steps, by default defined by a (truncated) Levy flight step length function. This particular algorithm is applied to mimic scale-free space use; i.e., Multi-scaled random walk. Merkle et al. have studied patch-to-patch distances, but this method obscures a test for degree of scale-free exploratory steps. By defining patch-to-patch movement they do for obvious reasons also find an approximately negative exponential distribution tail of such lengths (Weibull function with shape parameter close to 1). Since a step is defined as the distance from the source meadow to the first encountered next meadow patch, this length distribution should a priori be expected to be a negative exponential in the tail part; i.e., apparently reflecting a scale-specific process. For example, long distance steps could be subjectively terminated if the real target was further out relative to the first-encountered patch. In Gautestad (2013) I illustrate some pitfalls leading to false verification of scale-specific space use from real scale-free movement.
Further, by defining patch-to-patch steps (meadow-to-meadow), any subsequent intra-patch exploratory steps up to next patch departure will obscure analysis of the frequency of return steps relative to exploratory steps. MRW assumes a relatively small return frequency relative to exploratory steps (the ρ ratio; see the illustration above) while Merkle et al. (2014) find ca 2/3 of steps targeting familiar patches relative to reaching previously unexplored meadow. In the bison analysis the actual definition of intra-patch movement may unintentionally have inflated this ratio substantially, since most Levy flight-like steps are relatively short. This means that estimating ρ requires more data details and another approach.
Hence, the very interesting analyses presented by Merkle et al. (2014; 2017) unfortunately does not cast light on any potentially scale-free property of bison movement. Future work could for example use the step length function studied from the original GPS series of fixes. By sub-sampling these series at different time resolutions (e.g., 3 hours, 10 hours, etc.) and spatial sub-sections (to study variations of the local CSSU estimates, for example, by differentiating between steps inside and outside of meadows) the MRW compliance – and applicability as a tool for ecological inference – could be illuminated. It would also be interesting to see degree of model compliance and parameter differences between the winter and summer season.
REFERENCES
Gautestad, A. O., I. Mysterud, and M. R. Pelton. 1998. Complex movement and scale-free habitat use: testing the multi-scaled home range model on black bear telemetry data. Ursus 10:219-234.
Gautestad, A. O. and I. Mysterud. 2005. Intrinsic scaling complexity in animal dispersion and abundance. The American Naturalist 165:44-55.
Gautestad, A. O. 2013. Lévy meets Poisson: a statistical artifact may lead to erroneous re-categorization of Lévy walk as Brownian motion. The American Naturalist 181:440-450.
Gautestad, A. O. 2015. Animal Space Use: Memory Effects, Scaling Complexity, and Biophysical Model Coherence. Dog Ear Publishing, Indianapolis.
Gautestad, A. O. and I. Mysterud. 1995. The home range ghost. Oikos 74:195-204.
Gautestad, A. O. and I. Mysterud. 2005. Intrinsic scaling complexity in animal dispersion and abundance. The American Naturalist 165:44-55.
Gautestad, A. O. and I. Mysterud. 2006. Complex animal distribution and abundance from memory-dependent kinetics. Ecological Complexity 3:44-55.
Gautestad, A. O. and A. Mysterud. 2013. The Lévy flight foraging hypothesis: forgetting about memory may lead to false verification of Brownian motion. Movement Ecology 1:1-18.
Merkle, J. A., D. Fortin and J. M. Morales. 2014. A memory-based foraging tactic reveals an adaptive mechanism for restricted space use. Ecology Letters 17:924–931.
Merkle, J. A., J. R. Potts and D. Fortin. 2017. Energy benefits and emergent space use patterns of an empirically parameterized model of memory-based patch selection. Oikos 126:185–195
Nabe-Nielsen, J., J. Tougaard, J. Teilmann, K. Lucke and M. C. Forckhammer. 2013. How a simple adaptive foraging strategy can lead to emergent home ranges and increased food intake. Oikos 122:1307-1316.
van Moorter, B., D. Visscher, S. Benhamou, L. Börger, M. S. Boyce and J.-M. Gaillard. 2009. Memory keeps you at home: a mechanistic model for home range emergence. Oikos 118:641-652.
In Merkle et al.’s simulation model; which is described by both a Lagrangian and a quasi-Eulerian variant (integro-difference equation, leading to similar results), animals use spatial and attribute memory to choose food patches based on three components: whether or not they have previously visited them, their reference point of patch profitability derived from recent foraging experience, and their memory of the profitability of each previously visited patch.
First, the results confirm home range as an emergent property of spatial memory. Animals returning to previously visited patches with a higher probability than path crossing by chance leads to constrained space use even without a central place attraction force or borderline repellence. In compliance with both MRW (Gautestad et al. 1998; Gautestad and Mysterud 2005) and other memory-implementing models (e.g., van Moorter 2009; Nabe-Nielsen et al. 2013) bison re-visits its memorized patches to a high degree.
Second, bison differentiates (to varying degree) between experienced patch profitability and the quality of the current patch when choosing which patch to return to. While the basic MRW formulation treats all previously visited locations along a path as equal (and thus let returns happen randomly), this “homogeneous environment” simplification is trivially extended with better realism by defining a heterogeneous habitat for the model execution (e.g., Gautestad and Mysterud 2013; see image below). In short, since patches with high profitability can be assumed to be positively correlated with longer local staying time, the MRW model’s Characteristic Scale of Space Use (CSSU) parameter can be defined to vary accordingly. Hence, the local path density (number of locations pr. unit area) in superior patches will tend to be higher than average density. Consequently, even when the animal returns randomly and with equal relative weight to any previous location along the total path, the target location for such return events will tend to be over-represented in high quality patches. Further, when averaging over all visited patches, the basic MRW model is assumed to represent the average CSSU for the given space use extent. Thus, when studying over-all space use properties rather than (for example) intra-home range patch selection, the basic MRW model with homogeneous environment (constant CSSU) satisfies the Occam’s razor principle.
Third, bison chose meadows visited far back in time as strongly as recently visited meadows. In other words, memory decay was small. This is also a basic property of MRW. However, it could trivially be extended by allowing for varying degree of memory decay through time-dependent return probability to previously visited locations (Gautestad and I. Mysterud 2006; Gautestad and A. Mysterud 2013).
Fourth, Merkle et al. (2017) argue well for space use where targeted (memory-based) returns should be expected to be combined with random exploration. “…a certain amount of random patch use is necessary to avoid frequent returns to relatively poor-quality patches, or avoid being caught in a relatively poor quality area of the landscape” (p185). Bison data confirm this mixture of targeted returns and exploratory bouts, in compliance also with the MRW model.
What is missing from the bison results? Unfortunately, in order to test if bison confirms MRW-like space use relative to other memory-based models the data needs to be analysed for other properties. For example, the basic MRW model has two main components; (1) occasional return to previously visited patches, and (2) exploratory steps, by default defined by a (truncated) Levy flight step length function. This particular algorithm is applied to mimic scale-free space use; i.e., Multi-scaled random walk. Merkle et al. have studied patch-to-patch distances, but this method obscures a test for degree of scale-free exploratory steps. By defining patch-to-patch movement they do for obvious reasons also find an approximately negative exponential distribution tail of such lengths (Weibull function with shape parameter close to 1). Since a step is defined as the distance from the source meadow to the first encountered next meadow patch, this length distribution should a priori be expected to be a negative exponential in the tail part; i.e., apparently reflecting a scale-specific process. For example, long distance steps could be subjectively terminated if the real target was further out relative to the first-encountered patch. In Gautestad (2013) I illustrate some pitfalls leading to false verification of scale-specific space use from real scale-free movement.
Further, by defining patch-to-patch steps (meadow-to-meadow), any subsequent intra-patch exploratory steps up to next patch departure will obscure analysis of the frequency of return steps relative to exploratory steps. MRW assumes a relatively small return frequency relative to exploratory steps (the ρ ratio; see the illustration above) while Merkle et al. (2014) find ca 2/3 of steps targeting familiar patches relative to reaching previously unexplored meadow. In the bison analysis the actual definition of intra-patch movement may unintentionally have inflated this ratio substantially, since most Levy flight-like steps are relatively short. This means that estimating ρ requires more data details and another approach.
Hence, the very interesting analyses presented by Merkle et al. (2014; 2017) unfortunately does not cast light on any potentially scale-free property of bison movement. Future work could for example use the step length function studied from the original GPS series of fixes. By sub-sampling these series at different time resolutions (e.g., 3 hours, 10 hours, etc.) and spatial sub-sections (to study variations of the local CSSU estimates, for example, by differentiating between steps inside and outside of meadows) the MRW compliance – and applicability as a tool for ecological inference – could be illuminated. It would also be interesting to see degree of model compliance and parameter differences between the winter and summer season.
REFERENCES
Gautestad, A. O., I. Mysterud, and M. R. Pelton. 1998. Complex movement and scale-free habitat use: testing the multi-scaled home range model on black bear telemetry data. Ursus 10:219-234.
Gautestad, A. O. and I. Mysterud. 2005. Intrinsic scaling complexity in animal dispersion and abundance. The American Naturalist 165:44-55.
Gautestad, A. O. 2013. Lévy meets Poisson: a statistical artifact may lead to erroneous re-categorization of Lévy walk as Brownian motion. The American Naturalist 181:440-450.
Gautestad, A. O. 2015. Animal Space Use: Memory Effects, Scaling Complexity, and Biophysical Model Coherence. Dog Ear Publishing, Indianapolis.
Gautestad, A. O. and I. Mysterud. 1995. The home range ghost. Oikos 74:195-204.
Gautestad, A. O. and I. Mysterud. 2005. Intrinsic scaling complexity in animal dispersion and abundance. The American Naturalist 165:44-55.
Gautestad, A. O. and I. Mysterud. 2006. Complex animal distribution and abundance from memory-dependent kinetics. Ecological Complexity 3:44-55.
Gautestad, A. O. and A. Mysterud. 2013. The Lévy flight foraging hypothesis: forgetting about memory may lead to false verification of Brownian motion. Movement Ecology 1:1-18.
Merkle, J. A., D. Fortin and J. M. Morales. 2014. A memory-based foraging tactic reveals an adaptive mechanism for restricted space use. Ecology Letters 17:924–931.
Merkle, J. A., J. R. Potts and D. Fortin. 2017. Energy benefits and emergent space use patterns of an empirically parameterized model of memory-based patch selection. Oikos 126:185–195
Nabe-Nielsen, J., J. Tougaard, J. Teilmann, K. Lucke and M. C. Forckhammer. 2013. How a simple adaptive foraging strategy can lead to emergent home ranges and increased food intake. Oikos 122:1307-1316.
van Moorter, B., D. Visscher, S. Benhamou, L. Börger, M. S. Boyce and J.-M. Gaillard. 2009. Memory keeps you at home: a mechanistic model for home range emergence. Oikos 118:641-652.