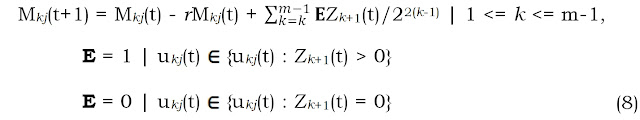Towards Complex Population Kinetics
Presented for the first time in my book, Multi-scaled random walk (MRW) hereby also has a complementary formulation for population kinetics, “the Zoomer model” (see Chapter 6. Modelling parallel processing). While population dynamics primarily is occupied with the time scale of seasons, years and generation times, population kinetics is typically also including the shorter time range of intra-season redistribution of individuals. In other words, this concept also covers higher-frequency and finer-grained spatio-temporal variability of a population’s distribution – as a mixture of intrinsic and extrinsic factors – in a more explicit manner than traditional population dynamical modelling.
If movement is “simple”, i.e., obeying classic diffusion laws and thus the mean field principle at the population level, the effect from individual-level system details may conveniently be “averaged out”, allowing for quite simply-structured models.
In physics and probability theory, mean field theory (MFT, also known as self-consistent field theory) studies the behavior of large and complex stochastic models by studying a simpler model. Such models consider a large number of small individual components which interact with each other. The effect of all the other individuals on any given individual is approximated by a single averaged effect, thus reducing a many-body problem to a one-body problem. (Wikipedia)
On the other hand, if individual-level movement is complex (e.g., scale-free and influenced by spatial memory in a non-Markovian manner), the mean field approximation should not a priori be expected to hold as a realistic representation of population dynamics.
Accounting for this shortcoming of the standard range of population models may have broad implications for population-dynamical modelling. As I describe in Chapter 1 of my book, classic tools like differential equations (temporally continuous dynamics, averaged over space), partial differential equations (dynamics in continuous time and space) and even coupled map lattice models (discrete time and space dynamics) may have to be substituted if space use is complex. Substituting with what? To my knowledge, there are no candidate models!
Thus, the Zoomer model represents the first (as far as I know) proposal for such a candidate model. It translates memory-influenced, scale-free space use at the individual level to the population level, in a statistical-mechanically coherent manner. The Zoomer model includes all the four standard BIDE rates (Birth, Immigration, Death and Emigration), and it is also spatially explicit. However, contrary to standard coupled map lattice models, spatial scale (the “lattice”) is implemented in a multi-scaled manner. This “scale range” approach allows for formulation of various aspects of complex population kinetics.
For example, the Zoomer model allows for explicit modelling of intraspecific cohesion (conspecific attraction), which is a complex process that depends on both temporal and spatial memory utilization at the individual level. In a simplified scenario, consider that a tendency for conspecific attraction is the main driver of the population kinetics. Further, consider that we study the process at sufficiently fine temporal and spatial scales to allow us to disregard the “slower” Birth and Death rates in the BIDE terms (it will be trivial to account for these processes as well, and I will do it in later posts). In other words, in this example focus is kept on one particular aspect of the intra-population redistribution process, the relatively high-pace influence from conspecific attraction on a populations spatial dispersion.
Consider that this attraction process takes place in parallel over a range (1, 2, …, k, .., m) spatial scales, where m is the defined maximum extent for memory-influenced “strategic” moves by the M individuals during the defined time increment from t to t+1. In this (simplified) scenario the Zoomer model for a population of Mkj individuals within respective set of virtual grid cells in a lattice of cell size size u at spatial scale level k can be summarized as:
During a given time increment a given fraction of the population (expressed by the rate r, which by default is identical at respective levels k) redistributes itself in self-organizing manner, leading to a statistically self-similar (“fractal”) distribution pattern over a range of spatial scales 1, …, m in compliance with the conceptual visualization in this post. However, in the present population-level example scenario the respective “zoomers” Z to respective scale levels k and in respective cells j at level k are collectively attracted towards their neighbourhood with the currently highest abundance of conspecifics at this scale (this neighbourhood thus receives all zoomers from its neighbourhood at this scale level during the given time increment; E=1 here and E=0 for the surrounding cells). Often the zoomers tend to return to the same neighbourhood, though, since this is where the pre-zooming abundance typically is largest. However, discovering a better location in the neighbourhood during zooming will lead to re-distribution of these individuals.
A complete description of this equation and its modifications for improved realism (e.g., the response to local overcrowding) is outside the scope of a single blog post. However, the model’s output seems to share many characteristics of real population kinetics. I will return to some examples in future posts.
In compliance with the parallel processing postulate for individual space use behaviour, as expressed by the Multi-scaled random walk (MRW) model, the Zoomer model is primarily developed to explore the process of population re-distribution of individuals over a local range of spatial scales. “Local” may cover quite a wide area, due to the model’s unique characterization of individual movement as a multi-scaled process (in analogy, consider the broad spatial range of the long tail of the step length distributuion from a Lévy walk, with the clear distinction that Lévy walk – as opposed to MRW – does not include spatial memory). At a temporal scale that is substantially smaller than the average reproduction cycle, movement of individuals determines adaptation to local ecological conditions – including conspecific abundance – to a larger extent than death and birth rates.
Like I advocated for the individual level modelling (see archive: "Homogeneous or Heterogeneous Environment?", January 30, 2016), it is a good approach to start exploring a new modelling concept under homogeneous simulation conditions to study the process’ intrinsic properties (in this case, the scale-free zoomer re-distribution potential), before turning towards increased complicatedness and realism by introducing environmental heterogeneity. However, often the dynamic and statistical response to the latter can quite trivially be deducted/predicted from the homogeneous condition.
If movement is “simple”, i.e., obeying classic diffusion laws and thus the mean field principle at the population level, the effect from individual-level system details may conveniently be “averaged out”, allowing for quite simply-structured models.
In physics and probability theory, mean field theory (MFT, also known as self-consistent field theory) studies the behavior of large and complex stochastic models by studying a simpler model. Such models consider a large number of small individual components which interact with each other. The effect of all the other individuals on any given individual is approximated by a single averaged effect, thus reducing a many-body problem to a one-body problem. (Wikipedia)
On the other hand, if individual-level movement is complex (e.g., scale-free and influenced by spatial memory in a non-Markovian manner), the mean field approximation should not a priori be expected to hold as a realistic representation of population dynamics.
Accounting for this shortcoming of the standard range of population models may have broad implications for population-dynamical modelling. As I describe in Chapter 1 of my book, classic tools like differential equations (temporally continuous dynamics, averaged over space), partial differential equations (dynamics in continuous time and space) and even coupled map lattice models (discrete time and space dynamics) may have to be substituted if space use is complex. Substituting with what? To my knowledge, there are no candidate models!
Thus, the Zoomer model represents the first (as far as I know) proposal for such a candidate model. It translates memory-influenced, scale-free space use at the individual level to the population level, in a statistical-mechanically coherent manner. The Zoomer model includes all the four standard BIDE rates (Birth, Immigration, Death and Emigration), and it is also spatially explicit. However, contrary to standard coupled map lattice models, spatial scale (the “lattice”) is implemented in a multi-scaled manner. This “scale range” approach allows for formulation of various aspects of complex population kinetics.
For example, the Zoomer model allows for explicit modelling of intraspecific cohesion (conspecific attraction), which is a complex process that depends on both temporal and spatial memory utilization at the individual level. In a simplified scenario, consider that a tendency for conspecific attraction is the main driver of the population kinetics. Further, consider that we study the process at sufficiently fine temporal and spatial scales to allow us to disregard the “slower” Birth and Death rates in the BIDE terms (it will be trivial to account for these processes as well, and I will do it in later posts). In other words, in this example focus is kept on one particular aspect of the intra-population redistribution process, the relatively high-pace influence from conspecific attraction on a populations spatial dispersion.
Consider that this attraction process takes place in parallel over a range (1, 2, …, k, .., m) spatial scales, where m is the defined maximum extent for memory-influenced “strategic” moves by the M individuals during the defined time increment from t to t+1. In this (simplified) scenario the Zoomer model for a population of Mkj individuals within respective set of virtual grid cells in a lattice of cell size size u at spatial scale level k can be summarized as:
During a given time increment a given fraction of the population (expressed by the rate r, which by default is identical at respective levels k) redistributes itself in self-organizing manner, leading to a statistically self-similar (“fractal”) distribution pattern over a range of spatial scales 1, …, m in compliance with the conceptual visualization in this post. However, in the present population-level example scenario the respective “zoomers” Z to respective scale levels k and in respective cells j at level k are collectively attracted towards their neighbourhood with the currently highest abundance of conspecifics at this scale (this neighbourhood thus receives all zoomers from its neighbourhood at this scale level during the given time increment; E=1 here and E=0 for the surrounding cells). Often the zoomers tend to return to the same neighbourhood, though, since this is where the pre-zooming abundance typically is largest. However, discovering a better location in the neighbourhood during zooming will lead to re-distribution of these individuals.
A complete description of this equation and its modifications for improved realism (e.g., the response to local overcrowding) is outside the scope of a single blog post. However, the model’s output seems to share many characteristics of real population kinetics. I will return to some examples in future posts.
In compliance with the parallel processing postulate for individual space use behaviour, as expressed by the Multi-scaled random walk (MRW) model, the Zoomer model is primarily developed to explore the process of population re-distribution of individuals over a local range of spatial scales. “Local” may cover quite a wide area, due to the model’s unique characterization of individual movement as a multi-scaled process (in analogy, consider the broad spatial range of the long tail of the step length distributuion from a Lévy walk, with the clear distinction that Lévy walk – as opposed to MRW – does not include spatial memory). At a temporal scale that is substantially smaller than the average reproduction cycle, movement of individuals determines adaptation to local ecological conditions – including conspecific abundance – to a larger extent than death and birth rates.
Like I advocated for the individual level modelling (see archive: "Homogeneous or Heterogeneous Environment?", January 30, 2016), it is a good approach to start exploring a new modelling concept under homogeneous simulation conditions to study the process’ intrinsic properties (in this case, the scale-free zoomer re-distribution potential), before turning towards increased complicatedness and realism by introducing environmental heterogeneity. However, often the dynamic and statistical response to the latter can quite trivially be deducted/predicted from the homogeneous condition.