Lab Mice Join the Zoomers Club
In a recent post I summarized the Zoomer model, a population level version of Multi-scaled random walk (MRW). Interestingly (in fact, thrillingly!) I just discovered a recent paper on the statistical properties of movement of the B6 strain of laboratory mice (Shoji 2016), which indirectly supports an important statistical-mechanical assumption both under the zoomer concept and the MRW.
Before turning towards movement of mice, I recap a basic property of the Zoomer model, and its coherence with the complementary individual-level process.
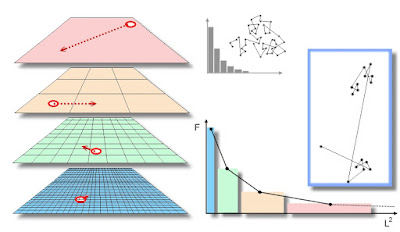
The illustration above is copied from Gautestad and Mysterud (2005), and illustrates the zoomer principle from the individual level; i.e., from the perspective of Multi-scaled random walk (MRW). To the left: individual zoomers are in the process of relocating themselves at length L at respective spatial scales (indicated by virtual grid resolutions) during a given time period T=M*t, where t is the unit time scale and series length M is large. Consider that t is small, meaning that we study the spatial relocation process at relatively high temporal frequency [in an upcoming post I elaborate on the effect from high versus low frequency. In the meantime I refer to my book, and to Gautestad (2012)].
However, assume that the unit time increment t is still large enough to allow for a sufficiently deep hidden layer to ensure a statistical-mechanical interpretation of the set of displacements, since both MRW and the Zoomer model rely on this framework. In other words, the arrows in the left-hand “sandwich” of scale levels reflect the individuals’ position at two successive points in time, but these relocation vectors do not reveal finer-grained moves at even finer time increments. Hence, the respective displacements cannot be interpreted mechanistically at this temporal resolution. Only the set as a whole (or subsets, if M is large enough) provides important information about the underlying space use behaviour, from the statistical-mechanical perspective.
To the right, the coloured graph shows the expected distribution F(L2) of number of zooming events to respective spatial scales during T, as revealed by a sample M. The spatial scale k on the abscissa is in this case expressed by a two-dimensional area unit, u = k2 ∝ L2 of respective virtual grid cells, and the bin intervals are scaling log-linearly (by comparison, the grey inset shows the expected – less fat-tailed – step length distribution from a scale-specific process, and thus presented with arithmetic bin intervals).
From a statistical-mechanical perspective, F(L2) may also represent the multi-scaled redistribution in a population sample of M individuals – a statistical “ensemble” – during a given time increment t (the zoomer model’s population perspective), rather than a given individual’s redistribution pattern at frequency M = T/t during T (the MRW perspective).
Observe that the area of each of the coloured rectangles in F(L2) is constant, meaning that the individual/population on average has distributed its space use intensity “uniformly” over the actual scale range. In other words, the ordinate and abscissa values for respective bins are inversely proportional. Uniformly distributed space use intensity over a scale range – the “equal weight” condition – is satisfied by the scaling parameter’s default value β=2 in the MRW model and by the complementary constant inter-scale redistribution rate r’ = r/(m-1) in the Zoomer model.
Now, let the statistical-mechanical Zoomer/MRW framework meet the real world. Is it realistic? In other words, what empirical evidence points towards this kind of cognitively driven scale-free space use?
First, we have the steadily accumulating support for scale-free movement, which for example may be Lévy walk or MRW. I refer to Gautestad (2012) and Gautestad and Mysterud (2013) for a proposed method to differentiate between these two universality classes (the classes are explained in The scaling cube post).
Second, by Hiroto Shoji’s results on movement by lab mice in a homogeneous field we now have an additional and complementary empirical zoomer support.
Shoji (2016), studied scale-free movement from the perspective of time scale rather than spatial scale. He explored apparatus size on rodent locomotor activity (the image to the right is copied from his paper), specifically with respect to how resting and walking periods are interwoven. When the diameter of the test apparatus was greater than 75 cm (and thus allowing for less influence from area constraint), the duration of both the resting and moving periods both obeyed bounded power-law distribution functions (like truncated Lévy walk).
Shoji’s aim was not to explore specific behavioural traits of movement from the present context of the zoomer/MRW framework, but incidentally it seems like his results have broader implications.
In particular, the scale-free “resting” period with a distribution log[F(resting)] with slope -1 was compliant with the zoomer/MRW model under the “equal weight” condition for multi-scaled space use. Thus, the mice showed similar cognitively driven multi-scaled behaviour as Cole (1995) found for Drosophila; a concept Cole termed “fractal time”, which he linked both to Lévy walk and to optimal foraging.
I put Shoji’s (2016) term “resting” in quotes, since these intervals were defined similarly as “patch staying times” in the ecological literature. In other words, the mouse had to show locomotion above a given threshold to count as “active” during the defined time increment. The “resting” periods for the mice then showed a scaling exponent typically in the range from -1.1 to -1.2.
Above I have again copied from Shoji (2016), but with an added twist. The inset shows an example of a distribution of displacement pr. unit time, measured in “pixel units”. I sampled this graph, and present here the result with log-log transformed axes. The log-log linearity confirms a scale-free distribution of step lengths.
I present the entire distribution, rather than focusing on the distribution below and above the threshold separately. Further, I interpret the “threshold” as a choice of spatio-temporal unit scales, u and t, in the Zoomer model.
According to the Zoomer/MRW model, displacements by a given individual from a given scale level u (the “threshold”, if you wish) to the next higher level u+1, should happen 1/u as often. In other words, the lab mouse example above satisfies this prediction. Since the environment in this experiment is homogeneous, the scaling behaviour is intrinsically driven. Also this system property satisfies the Zoomer/MRW model, since it complies with the parallel processing postulate for multi-scaled space use.
The slope from the mouse’s distribution is not exactly -1, showing a power exponent of circa -1.12. According to the Zoomer/MRW framework, a steeper slope (but still log-log linear) simply implies that the animal(s) has/have skewed its/their space use utilization slightly towards finer scales, on expense of coarser scales, but still in a scale-free manner. A slope of exactly -1 only represents the default Zoomer/MRW condition; i.e., the ideal model.
The classic Markov-based framework for animal movement and population redistribution does not predict log-log linearity in the graph above, but a steadily steeper slope with increasing abscissa value; in other words, a negative exponential function (see grey inset in the first illustration in this post, but observe its arithmetic axes).
Thanks to Shoji’s experiment, both MRW and the Zoomer model seems to have found additional support from behavioural studies on real animals.
REFERENCES
Cole, B. J. (1995) Fractal time in animal behaviour: the moment activity of Drosophila. Anim. Behav., 50, 1317-1324.
Gautestad, A. O. (2012) Brownian motion or Lévy walk? Stepping towards an extended statistical mechanics for animal locomotion. Journal of the Royal Society Interface, 9, 2332-2340.
Gautestad, A. O. & Mysterud, I. (2005) Intrinsic scaling complexity in animal dispersion and abundance. The American Naturalist, 165, 44-55.
Gautestad, A. O. & Mysterud, A. (2013) The Lévy flight foraging hypothesis: forgetting about memory may lead to false verification of Brownian motion. Movement Ecology, 1, 1-18.
Shoji, H. (2016) Scaling law in free walking of mice in circular open fields of various diameters. J. Biol. Phys., DOI: 10.1007/s10867-015-9406-z.
Before turning towards movement of mice, I recap a basic property of the Zoomer model, and its coherence with the complementary individual-level process.
However, assume that the unit time increment t is still large enough to allow for a sufficiently deep hidden layer to ensure a statistical-mechanical interpretation of the set of displacements, since both MRW and the Zoomer model rely on this framework. In other words, the arrows in the left-hand “sandwich” of scale levels reflect the individuals’ position at two successive points in time, but these relocation vectors do not reveal finer-grained moves at even finer time increments. Hence, the respective displacements cannot be interpreted mechanistically at this temporal resolution. Only the set as a whole (or subsets, if M is large enough) provides important information about the underlying space use behaviour, from the statistical-mechanical perspective.
To the right, the coloured graph shows the expected distribution F(L2) of number of zooming events to respective spatial scales during T, as revealed by a sample M. The spatial scale k on the abscissa is in this case expressed by a two-dimensional area unit, u = k2 ∝ L2 of respective virtual grid cells, and the bin intervals are scaling log-linearly (by comparison, the grey inset shows the expected – less fat-tailed – step length distribution from a scale-specific process, and thus presented with arithmetic bin intervals).
From a statistical-mechanical perspective, F(L2) may also represent the multi-scaled redistribution in a population sample of M individuals – a statistical “ensemble” – during a given time increment t (the zoomer model’s population perspective), rather than a given individual’s redistribution pattern at frequency M = T/t during T (the MRW perspective).
Observe that the area of each of the coloured rectangles in F(L2) is constant, meaning that the individual/population on average has distributed its space use intensity “uniformly” over the actual scale range. In other words, the ordinate and abscissa values for respective bins are inversely proportional. Uniformly distributed space use intensity over a scale range – the “equal weight” condition – is satisfied by the scaling parameter’s default value β=2 in the MRW model and by the complementary constant inter-scale redistribution rate r’ = r/(m-1) in the Zoomer model.
Now, let the statistical-mechanical Zoomer/MRW framework meet the real world. Is it realistic? In other words, what empirical evidence points towards this kind of cognitively driven scale-free space use?
First, we have the steadily accumulating support for scale-free movement, which for example may be Lévy walk or MRW. I refer to Gautestad (2012) and Gautestad and Mysterud (2013) for a proposed method to differentiate between these two universality classes (the classes are explained in The scaling cube post).
Shoji (2016), studied scale-free movement from the perspective of time scale rather than spatial scale. He explored apparatus size on rodent locomotor activity (the image to the right is copied from his paper), specifically with respect to how resting and walking periods are interwoven. When the diameter of the test apparatus was greater than 75 cm (and thus allowing for less influence from area constraint), the duration of both the resting and moving periods both obeyed bounded power-law distribution functions (like truncated Lévy walk).
Shoji’s aim was not to explore specific behavioural traits of movement from the present context of the zoomer/MRW framework, but incidentally it seems like his results have broader implications.
In particular, the scale-free “resting” period with a distribution log[F(resting)] with slope -1 was compliant with the zoomer/MRW model under the “equal weight” condition for multi-scaled space use. Thus, the mice showed similar cognitively driven multi-scaled behaviour as Cole (1995) found for Drosophila; a concept Cole termed “fractal time”, which he linked both to Lévy walk and to optimal foraging.
I put Shoji’s (2016) term “resting” in quotes, since these intervals were defined similarly as “patch staying times” in the ecological literature. In other words, the mouse had to show locomotion above a given threshold to count as “active” during the defined time increment. The “resting” periods for the mice then showed a scaling exponent typically in the range from -1.1 to -1.2.
I present the entire distribution, rather than focusing on the distribution below and above the threshold separately. Further, I interpret the “threshold” as a choice of spatio-temporal unit scales, u and t, in the Zoomer model.
According to the Zoomer/MRW model, displacements by a given individual from a given scale level u (the “threshold”, if you wish) to the next higher level u+1, should happen 1/u as often. In other words, the lab mouse example above satisfies this prediction. Since the environment in this experiment is homogeneous, the scaling behaviour is intrinsically driven. Also this system property satisfies the Zoomer/MRW model, since it complies with the parallel processing postulate for multi-scaled space use.
The slope from the mouse’s distribution is not exactly -1, showing a power exponent of circa -1.12. According to the Zoomer/MRW framework, a steeper slope (but still log-log linear) simply implies that the animal(s) has/have skewed its/their space use utilization slightly towards finer scales, on expense of coarser scales, but still in a scale-free manner. A slope of exactly -1 only represents the default Zoomer/MRW condition; i.e., the ideal model.
The classic Markov-based framework for animal movement and population redistribution does not predict log-log linearity in the graph above, but a steadily steeper slope with increasing abscissa value; in other words, a negative exponential function (see grey inset in the first illustration in this post, but observe its arithmetic axes).
Thanks to Shoji’s experiment, both MRW and the Zoomer model seems to have found additional support from behavioural studies on real animals.
REFERENCES
Cole, B. J. (1995) Fractal time in animal behaviour: the moment activity of Drosophila. Anim. Behav., 50, 1317-1324.
Gautestad, A. O. (2012) Brownian motion or Lévy walk? Stepping towards an extended statistical mechanics for animal locomotion. Journal of the Royal Society Interface, 9, 2332-2340.
Gautestad, A. O. & Mysterud, I. (2005) Intrinsic scaling complexity in animal dispersion and abundance. The American Naturalist, 165, 44-55.
Gautestad, A. O. & Mysterud, A. (2013) The Lévy flight foraging hypothesis: forgetting about memory may lead to false verification of Brownian motion. Movement Ecology, 1, 1-18.
Shoji, H. (2016) Scaling law in free walking of mice in circular open fields of various diameters. J. Biol. Phys., DOI: 10.1007/s10867-015-9406-z.