Lévy Walking or Not Lévy Walking – That’s the Question
As summarized and reviewed by many, one of the hot topics in the field of movement ecology regards to what extent – and under which ecological conditions – an animal performs scale-free movement. As readers of my book and my blog definitely have observed, I advocate a distinction between several kinds of scale-free movement (summarized by the Scaling cube); in particular, (a) the standard battleground of Lévy walk vs. Brownian motion (scale-free vs. scale-specific movement) (b) Lévy walk vs. composite random walk (a “Lévy walk look-alike”, i.e., pseudo-scale-free movement), and (c) Multi-scaled random walk (MRW; scale-free movement with site fidelity). The third variant has so far not received much attention in this debate. This is in my view unfortunate, because this approach apparently has the potential to resolve much of the controversy!
It is a fact that empirical research on scale-free vs. scale-specific movement generally has ignored the effect from animal site fidelity. This important and very universal property of animal space use seems to have got lost in convoluted and heated discussions on statistical methods and statistical interpretation of results. Why is this unfortunate? Simply because an inclusion of site fidelity when modeling space use allows a given movement pattern to appear scale-free or scale-specific, simply as a function of sampling frequency.
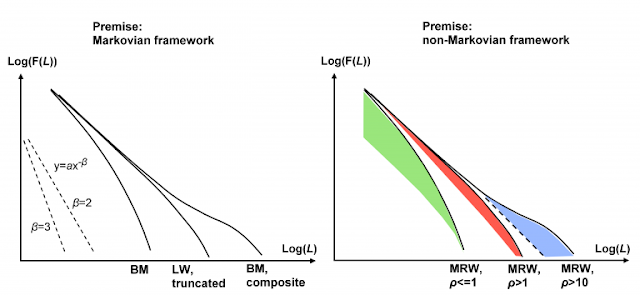
Research in this field tends to focus on the Lagrangian aspect of scale-free vs. scale-specific movement; i.e., the distribution F(L) of inter-fix displacement lengths L in a set of relocations from sampling at interval t along the true path. Based on our simulation results, a visual inspection of F(L) may apparently give a good clue about the actual generating process, as illustrated conceptually by the three classic candidate models in the left-hand part of the illustration above (the Figure is copied from Gautestad and Mysterud, 2013). For example, with log-transformed axes, linearity over a range of 10-100 length units is needed to make the distribution acceptable as statistically “scale-free” and thus Lévy walk compliant over this range, based on a first visual inspection (more formal MLE statistics will then typically confirm this). Such linearity implies a power law distribution, with log-log slope of magnitude –β and 1<β<3.
As the slope becomes steeper than -3 in log-log plot, the data is most likely reflecting scale-specific movement – apparently! Why “apparently”? Because the standard set of candidate models all define this specific transition as a critical magnitude of β to distinguish scale-free from scale-specific movement, without considering the influence from the sampling frequency 1/t; i.e., without considering a site fidelity effect on observed β.
The traditional set of models are implicitly based on an assumption that the animal’s path is not influenced by site fidelity. In other words, the animal is assumed to self-cross its historic path by chance only. Very unlikely, under a broad range of ecological conditions! MRW, which in my view should be included in the set of candidate models in this melting pot, will force upon the analysis a modification of how this scale-specific/scale-free transition at β≈3 is interpreted. In the MRW model, scale-free space use is combined with site fidelity. At present, MRW is the only model that provides this combination!
Site fidelity implies a sensitivity to sampling frequency. If 1/t is substantially larger (interval smaller) than the animal’s average return frequency towards previously visited locations, we do not expect much effect from site fidelity on the distribution F(L). There is only a minute chance for a return event taking place during a given sampling interval. The MRW process will at these temporal resolutions appear scale-free and Lévy walk compliant. However, if the ratio ρ between the animal’s average return interval and the researcher’s choice of sampling interval is approaching unit size from above – and perhaps even passing over to ρ<1 (high probability of at least one return event during t) – the distribution F(L) will no longer look scale-free. Under this condition the effect from spatial memory on space use comes into focus and will tend to blur any log-log linearity in the F(L) distribution.
The site fidelity effect is illustrated in the right-hand part of the image above. At high frequency sampling relative to the individual’s average return interval, the effect from return events – the site fidelity effect – is basically concentrated in the outermost part of the tail of the distribution (blue area). In the MRW model, this “hump” pattern is reflecting that return events, whenever they have happened during a sampling interval, will tend to produce a quite large displacement at the next relocation in the series, relative to the median step length from sampled displacements that are void of such returns. Next, consider that ρ is decreased from e.g. 100 towards a smaller ratio using a larger t. For example, in the range 1<ρ<10 simulations show that the slope may be “artificially” steepened by the site fidelity effect, making the functional form increasingly similar to a truncated Levy walk as ρ →1. A statistical analysis may be expected to show a somewhat reduced β in the small-L range and an increased β in the large-L range. Under this condition the influence from return events become more broadly distributed over the F(L) range (red area). When ρ<1, F(L) may give the impression of Brownian motion compliance due to a concentration of return steps in the left-hand part of the distribution (green area).
It seems like a distributional mixture in the zone between truncated Lévy walk and Brownian motion is the typical pattern observed in real F(L) distributions, making it appear like an animal that my be mode-shifting between truncated Lévy walk and Brownian motion. However, considering the alternative MRW model introduces another interpretation: the movement could potentially be scale-free under influence of site fidelity, which makes the functional form of F(L) observer-dependent. The latter implies that F(L) becomes a function of ρ (where the observer defines the denominator). Based on the typically observed intermittent appearance of F(L) in real data, the discussion continues circling back and forth, year after year: is the pattern complying best with truncated Lévy walk, or a scale-specific Brownian motion? Adding MRW to the set of candidate models for Bayesian analysis might perhaps resolve the gridlock and bring us closer to consensus?
It should be easy enough to test MRW’s potential strength in this regard, given a sufficiently large data set, collected over a sufficiently high sampling frequency. Studying the effect on F(L) from different ρ then becomes a matter of sub-sampling the series.
Both truncated Lévy walk and MRW will show a steepened slope upon such sub-sampling, but these two alternative hypotheses may be easily distinguished by supplementing the F(L) analysis with fractal analysis of the spatial fix pattern (MRW will maintain D≈1, while truncated LW will tend towards larger D). One could also look for the home range ghost (incidence increasing proportionally with √N for MRW and incidence increasing proportionally with N for LW).
When ρ>≈10, simulations of MRW show that return events tend to inflate the occurrence of very long steps, giving the impression of a “hump”, for example as shown above for at ρ≈10. Several researchers in the field of Lévy research have in fact anecdotally observed such a hump, without having a plausible behavioural explanation for it within the context of the traditional candidate models. However, if ρ>>10, the hump may in the MRW scenario almost disappear, making F(L) even more Lévy-like. The illustration to the right shows the simulation result for ρ=100 (Gautestad and Mysterud, 2013).
Already in Gautestad and Mysterud (2005) we illustrated the ρ effect on the “problematic” F(L) distribution. In Gautestad and Mysterud (2013) we elaborated further on this aspect. However, so far it looks like nobody has grasped this approach to see to what extent this “process-oriented” MRW framework might contribute to bringing the controversy out of the quagmire. In the meantime, the Lévy controversy rolls on, based on models void of spatial memory effects on F(L).
The MRW approach might also contribute to resolve other hot topics in movement ecology. For example, according to the Lévy walk/flight hypothesis for optimal foraging (a more specific aspect of the issue outlined above), Brownian motion is expected in an environment with a relatively productive environment with a relatively predictable resource distribution. In contrast, the MRW working hypothesis would be: in an environment with a relatively productive environment the individual’s home range is expected to be smaller, due to higher return frequency (stronger site fidelity, and thus a smaller ρ for a given sampling frequency). Hence, based on MRW one may predict that the site fidelity effect on F(L) will be more pronounced under these circumstances. If observation frequency, 1/t, is not increased accordingly, one may erroneously find support for the Levy flight foraging hypothesis. Supplementary test should be performed before concluding.
REFERENCES
Gautestad, A. O., and I. Mysterud. 2005. Intrinsic scaling complexity in animal dispersion and abundance. The American Naturalist 165:44-55.
Gautestad, A. O., and A. Mysterud. 2013. The Lévy flight foraging hypothesis: forgetting about memory may lead to false verification of Brownian motion. Movement Ecology 1:1-18.
It is a fact that empirical research on scale-free vs. scale-specific movement generally has ignored the effect from animal site fidelity. This important and very universal property of animal space use seems to have got lost in convoluted and heated discussions on statistical methods and statistical interpretation of results. Why is this unfortunate? Simply because an inclusion of site fidelity when modeling space use allows a given movement pattern to appear scale-free or scale-specific, simply as a function of sampling frequency.
As the slope becomes steeper than -3 in log-log plot, the data is most likely reflecting scale-specific movement – apparently! Why “apparently”? Because the standard set of candidate models all define this specific transition as a critical magnitude of β to distinguish scale-free from scale-specific movement, without considering the influence from the sampling frequency 1/t; i.e., without considering a site fidelity effect on observed β.
The traditional set of models are implicitly based on an assumption that the animal’s path is not influenced by site fidelity. In other words, the animal is assumed to self-cross its historic path by chance only. Very unlikely, under a broad range of ecological conditions! MRW, which in my view should be included in the set of candidate models in this melting pot, will force upon the analysis a modification of how this scale-specific/scale-free transition at β≈3 is interpreted. In the MRW model, scale-free space use is combined with site fidelity. At present, MRW is the only model that provides this combination!
Site fidelity implies a sensitivity to sampling frequency. If 1/t is substantially larger (interval smaller) than the animal’s average return frequency towards previously visited locations, we do not expect much effect from site fidelity on the distribution F(L). There is only a minute chance for a return event taking place during a given sampling interval. The MRW process will at these temporal resolutions appear scale-free and Lévy walk compliant. However, if the ratio ρ between the animal’s average return interval and the researcher’s choice of sampling interval is approaching unit size from above – and perhaps even passing over to ρ<1 (high probability of at least one return event during t) – the distribution F(L) will no longer look scale-free. Under this condition the effect from spatial memory on space use comes into focus and will tend to blur any log-log linearity in the F(L) distribution.
The site fidelity effect is illustrated in the right-hand part of the image above. At high frequency sampling relative to the individual’s average return interval, the effect from return events – the site fidelity effect – is basically concentrated in the outermost part of the tail of the distribution (blue area). In the MRW model, this “hump” pattern is reflecting that return events, whenever they have happened during a sampling interval, will tend to produce a quite large displacement at the next relocation in the series, relative to the median step length from sampled displacements that are void of such returns. Next, consider that ρ is decreased from e.g. 100 towards a smaller ratio using a larger t. For example, in the range 1<ρ<10 simulations show that the slope may be “artificially” steepened by the site fidelity effect, making the functional form increasingly similar to a truncated Levy walk as ρ →1. A statistical analysis may be expected to show a somewhat reduced β in the small-L range and an increased β in the large-L range. Under this condition the influence from return events become more broadly distributed over the F(L) range (red area). When ρ<1, F(L) may give the impression of Brownian motion compliance due to a concentration of return steps in the left-hand part of the distribution (green area).
It should be easy enough to test MRW’s potential strength in this regard, given a sufficiently large data set, collected over a sufficiently high sampling frequency. Studying the effect on F(L) from different ρ then becomes a matter of sub-sampling the series.
Both truncated Lévy walk and MRW will show a steepened slope upon such sub-sampling, but these two alternative hypotheses may be easily distinguished by supplementing the F(L) analysis with fractal analysis of the spatial fix pattern (MRW will maintain D≈1, while truncated LW will tend towards larger D). One could also look for the home range ghost (incidence increasing proportionally with √N for MRW and incidence increasing proportionally with N for LW).
Already in Gautestad and Mysterud (2005) we illustrated the ρ effect on the “problematic” F(L) distribution. In Gautestad and Mysterud (2013) we elaborated further on this aspect. However, so far it looks like nobody has grasped this approach to see to what extent this “process-oriented” MRW framework might contribute to bringing the controversy out of the quagmire. In the meantime, the Lévy controversy rolls on, based on models void of spatial memory effects on F(L).
The MRW approach might also contribute to resolve other hot topics in movement ecology. For example, according to the Lévy walk/flight hypothesis for optimal foraging (a more specific aspect of the issue outlined above), Brownian motion is expected in an environment with a relatively productive environment with a relatively predictable resource distribution. In contrast, the MRW working hypothesis would be: in an environment with a relatively productive environment the individual’s home range is expected to be smaller, due to higher return frequency (stronger site fidelity, and thus a smaller ρ for a given sampling frequency). Hence, based on MRW one may predict that the site fidelity effect on F(L) will be more pronounced under these circumstances. If observation frequency, 1/t, is not increased accordingly, one may erroneously find support for the Levy flight foraging hypothesis. Supplementary test should be performed before concluding.
REFERENCES
Gautestad, A. O., and I. Mysterud. 2005. Intrinsic scaling complexity in animal dispersion and abundance. The American Naturalist 165:44-55.
Gautestad, A. O., and A. Mysterud. 2013. The Lévy flight foraging hypothesis: forgetting about memory may lead to false verification of Brownian motion. Movement Ecology 1:1-18.